PETER KLICHE - Mathematik und Technik


	Gegenüberliegende Winkel im Sehnenviereck

	siehe auch Wikibooks Wikipedia (Die freie Enzyklopädie)

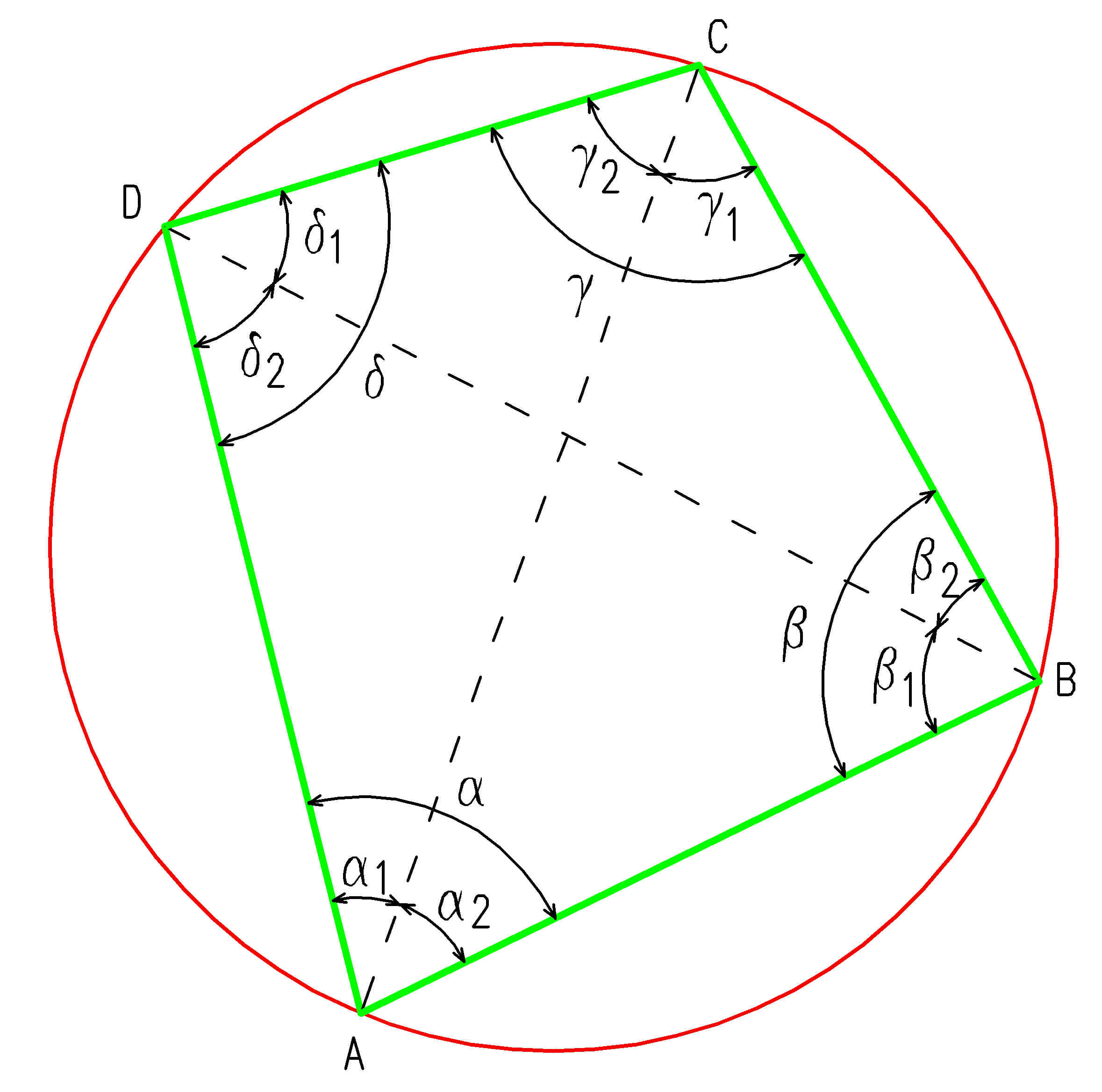
	Im Sehnenviereck beträgt die Winkelsumme der gegenüberliegenden Winkel 180°.

	Die läßt sich wie folgt beweisen:


	Winkelsumme im Dreieck ABD
	$\, \alpha + \beta _1 + \delta _2 = 180^0$

	Umfangswinkel über Sehne AB sind gleich
	$\, \delta _2 = \gamma _1$

	Umfangswinkel über Sehne AD sind gleich
	$\, \delta _2 = \gamma _1$

	eingesetzt ergibt sich
	$\, \alpha + \gamma _2 + \gamma _1 = 180^0$

	mit
	$\, \gamma = \gamma _1 + \gamma _2$

	deshalb ist
	$\, \alpha + \gamma = 180^0$

	Analog ist deshalb auch
	$\, \beta + \delta = 180^0$


Homepage \| Impressum \| Kontakt \| Über mich \| Datenschutz