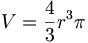PETER KLICHE

 

 

 

 

 

 

 

 

 

Rauminhalt der Kugel

 

 

 

 

Nachfolgend wird eine Ableitung für das Kugelvolumen dargestellt:

Nach Archimedes wird der Nachweis über die Berechnung eines Zylinder- und eines Kegelinhalts geführt. Man nimmt einen Zylinder dessen Grundfläche den Durchmesser der zu berechnenden Kugel hat und dessen Höhe den Radius der Kugel hat. In diesen Zylinder legt man einen Kegel, dessen Spitze im Mittelpunkt des unteren Grundkreises des Zylinders liegt und dessen Grundfläche mit der oberen Grundfläche des Zylinders identisch ist. Nun kann man nachweisen, dass das Differenzvolumen dieser beiden Körper (Zylinder minus Kegel) gleich dem Volumen der Halbkugel mit dem gleichen Durchmesser ist. Schneidet man nämlich beide Körper in einer beliebigen Höhe y ergeben sich als Schnittfläche für die Halbkugel eine Kreisfläche und für den Restkörper ein Kreisring. Diese Flächen sind gleich groß (siehe Skizze) und damit muss auch das Volumen gleich sein.

 

 

 

 

 

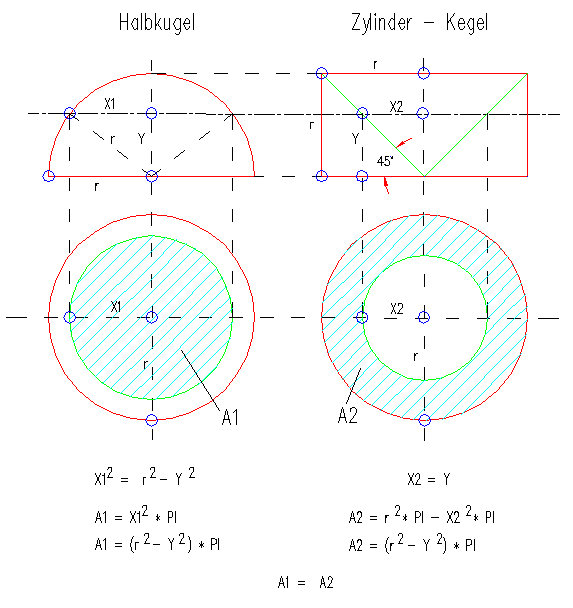
Aus dem Differenzvolumen Zylinder – Kegel kann man nun schnell die Kugelformel ermitteln:

Zylinder:

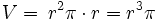
V = \frac{}{}r^2\pi \cdot r = r^3\pi

Kegel:

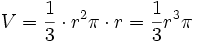
V = \frac{1}{3} \cdot r^2\pi \cdot r = \frac{1}{3}r^3\pi

Restkörper (= Halbkugel):

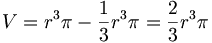
V = r^3\pi - \frac{1}{3}r^3\pi = \frac{2}{3}r^3\pi

Damit ist das Volumen der Vollkugel:

V = \frac{4}{3}r^3\pi